Validation of a High Resolved SSM/I Sea Ice Algorithm
using Airborne and ERS-2 SAR Data and Atmospheric Models.
Submitted to the Canadian Journal of Remote Sensing - Focus Issue on Ice and Icebergs
Lars Kaleschke, Christof Lüpkes, Timo Vihma, Jörg Haarpaintner, Axel Bochert, Jörg Hartmann, Georg Heygster
Lars Kaleschke, Georg Heygster
Institute of Environmental Physics, University Bremen, Bremen
Christof Lüpkes, Axel Bochert, Jörg Hartmann
Alfred Wegener Institute for Polar and Marine Research, Bremerhaven, Germany
Jörg Haarpaintner
Norwegian Polar Institute, Polarmiljosenteret, N-9296 Tromso, Norway
Timo Vihma
Finnish Institute of Marine Research, Helsinki, Finland
Contact: Lars Kaleschke
Institute of Environmental Physics,
P.O. Box 33 04 40, D-28334 Bremen, Germany
Phone: +49(0)421 218-4726, FAX: -4555
e-mail: Lars@Seaice.de, web-site: http://www.seaice.de
Abstract
Two algorithms have been used in a hybrid scheme in order
to obtain sea ice concentration maps at 12 km resolution
from 19, 37, and 85 GHz SSM/I data.
The first one is an algorithm based on the polarization
difference near 90 GHz and the second one is the NASA
Team algorithm which uses the 19 and 37 GHz SSM/I channels.
Ice concentrations are calculated using the 85 GHz channels.
In addition, the lower frequency channels are used to decide
whether the data points belong to the ice-free ocean or to
the ice-covered area. This combination eliminates
incorrect high ice concentrations caused by weather effects
over the ice-free ocean. It uses the rather weather
independent low frequencies while retaining high resolution
over ice with the high frequency.
A statistical linear regression
method for reference brightness temperature estimation was applied
in order to avoid misarranged guesses of the tie points.
This method requires independent ice concentration
reference data which were derived from
aircraft dual-polarized passive microwave
measurements at 19 and 37 GHz and optical line scanner images.
ERS-2 SAR images were used to analyze the capability
of the SSM/I to resolve features such as the evolution of
the marginal ice zone in the Fram Strait and the Storfjorden Polynya.
Two different numerical atmospheric models were used to analyze the
effect of an increased resolution of ice data from 50 to 12 km
on the model results.
It was found that the representation of the ice edge zone
significantly influences the modelled atmospheric boundary-layer
temperatures. The temperatures obtained with the high
resolution ice data agree significantly better with
airborne data.
1. Introduction
For about thirty years microwave remote sensing techniques
have been used for sea ice observations.
Advances in satellite sensor technology have led to a
considerable improvement of spatial resolution and accuracy
of the measured quantities.
Maps of the sea ice concentration are useful for
ship navigation as well as for use in models of the Earth's climate system
and the regional weather.
The spatial resolution of numerical models describing different
components of the Earth's climate system,
the ocean, atmosphere, and cryosphere,
is more and more increasing. Regional atmospheric
models now have a resolution of 1/6 degree (18.5 km).
Process studies have been carried out with mesoscale models
in polar regions at even finer horizontal resolutions of 4 km
(e.g. Vihma, 1995; Birnbaum and Lüpkes, submitted).
The heat and momentum fluxes at the boundary of
atmosphere and ocean significantly depend on the
ice concentration (Ledley, 1988).
This is especially true during winter when the temperature difference between
near-surface cold air and the surface of open water within
the Arctic pack ice or in the marginal sea ice zone (MIZ) can reach up to
40 K. Under such conditions strong ice production occurs (Cavalieri and
Martin, 1994). During the ice formation two thirds of the initial water
salinity are being released as brine (Martin and Kauffman, 1981).
Because the released brine is denser than the surrounding water masses,
it sinks and induces convection in the ocean (Aagaard and Carmack, 1989).
This paper is based on results of the
Arctic Radiation and Turbulence Interaction STudy (ARTIST),
which was conducted in the environment of the Svalbard archipelago
in March and April 1998.
The core activity of the ARTIST project was an extensive
field study with ground based and airborne measurements
accompanied by adequate model experiments.
A comprehensive description of the ARTIST work
can be found in Hartmann et al. (1999)
or at the ARTIST web-site (ARTIST).
The section of the Storfjorden Polynya was a result of
independent work, which was not part of the ARTIST project.
The goal of our study is the developement of an
improved method for the production of sea ice concentration
maps with 12 km resolution
derived from satellite passive microwave data
and to demonstrate the benefits from the high
resolution for model experiments.
We first outline the relevant data sources,
the ARTIST aircraft measurements, and the
satellite observations from Special Sensor
Microwave Imager (SSM/I)
and synthetic aperture radar on board
the second European Remote Sensing Satellites (ERS-2 SAR)
(section 2).
Then we present a hybrid algorithm based mainly on
Svendsen's et al. (1987) model for deriving ice concentration
from near 90 GHz satellite passive microwave data
and a new method for
deriving dedicated reference brightness temperatures
(tie points) for sea ice and open water (section 4).
The tie points for the hybrid algorithm are derived in
section 5 using aircraft data and used to
calculate ice concentrations.
After that we compare the results to those of the
NASA Team algorithm, which was applied to
aircraft as well as satellite data.
Next we interprete the results
of the hybrid algorithm using ERS-2 SAR images (section 6).
Finally the results serve to investigate the sensitivity of
atmospheric models to the sea ice
concentration (section 7).
2. Data set
During ARTIST several satellite under-flights were carried out
with the research aircraft Polar 2 and Polar 4
of the Alfred Wegener Institute for Polar and
Marine Research (AWI) while operating
equipment for remote sensing.
This equipment consists of microwave radiometers,
line scanners, radiation thermometer, and
a laser altimeter, as well as several sensors for measuring
meteorological parameters.
The non-imaging dual-polarized 19 and 37 GHz
radiometers used in Polar 4 allow to scan the surface
below the aircraft at an incidence angle of 53° similar
to the viewing geometry of the SSM/I.
The spatial resolution of the aircraft data is much higher
(100-200 m) than that of the SSM/I data (12-50 km).
The aircraft remote sensing measurements are used for a direct comparison with
the satellite data. The aircraft in-situ measurements (air temperature,
humidity, pressure, wind) are used in the modelling studies in section 7 to
assess the effect of the improved accuracy of the ice cover on
the development of the atmospheric boundary layer.
The SSM/I sensor is a passive microwave radiometer.
It has been launched as part of the Defense Meteorological Satellite Program (DMSP)
on the series of DMSP F-x satellites.
The SSM/I measures dual polarized microwave radiances at 19, 37 and 85 GHz
and vertically polarized radiances at 22 GHz.
The SSM/I scans the Earth's surface conically with a
swath of 1400 km width. Thus the SSM/I, operating from a near-polar
orbit, provides an almost global coverage every day.
The sampling distance is 12.5 km at the 85 GHz channels and 25 km
at the other channels.
The spatial resolution depends on the frequency (Table 1)
because the SSM/I utilizes only one broad-band antenna and
the spatial resolution is determined by diffraction.
The ERS-2 SAR gains
surface information in very high spatial
resolution of about 25 m, within a 100 km wide swath
and with limited temporal access.
The ERS-2 SAR operates at a frequency of 5.3 GHz (C-band) at an
incidence angle of about 23° with VV-polarization
(vertical on transmit, vertical on receive) (Kramer, 1996).
For ARTIST, we acquired 40 ERS-2 SAR images
partly coincident with the aircraft flights.
Table 1: Effective field of view of the SSM/I channels. (Hollinger, 1990)
| Frequency [GHz] |
Resolution [km²] |
| 19.35 | 69 x 43 |
| 22.235 | 60 x 40 |
| 37.0 | 37 x 29 |
| 85.5 | 15 x 13 |
3. SSM/I Algorithms
Several algorithms exist to derive the area fraction of ice
coverage from SSM/I data. The differences between the techniques
consist primarily in a different choice and utilization of the sensor channels,
in different tie points.
The NASA Team algorithm (NTA) is widely used
and was therefore selected
as a reference in this study
(Cavalieri et al., 1984; Cavalieri et al. 1991).
It makes use of both frequency and
polarization information at 19 and 37 GHz.
The spatial and temporal variations of the ice
temperature are taken into account in the NTA to the
first order by using the polarization ratio (PR) and the spectral
gradient ratio (GR) which aredefined by
PR=[TB(19V)-TB(19H)]/[TB(19V)+TB(19H)] (1)
GR=[TB(37V)-TB(19V)]/[TB(37V)+TB(19V)] (2)
where, for instance, TB(19V) is the vertically polarized
brightness temperature at 19 GHz, and H refers to horizontal polarization.
The two nearly independent parameters PR and GR are used to
solve a mixing equation for the three dominant ocean surface
types of the Arctic: open water, first-year and multiyear ice.
Comparisons of the NTA to several other 19 and 37 GHz based
algorithms, conducted for instance by Burns (1993)
and Comiso et al. (1997), reveal discrepancies
of up to 45% in the ice concentration values.
The NTA has a few shortcomings, for instance the
underestimation of the ice concentration in presence of new
ice and the low resolution of the 19 GHz channels.
Recently, the NTA was enhanced by Markus and Cavalieri (2000)
in order to overcome the problem of a bias towards lower
ice concentrations associated with snow surface effects.
The revised algorithm (NT2) includes the 85 GHz channels,
which are less sensitive to inhomogenities inside
the snow. The NT2 algorithm has not been used
in this study due to the lack of 85 GHz aircraft
measurements.
The 85 GHz SSM/I channels yield considerably higher resolution
than the other SSM/I channels.
However, the atmosphere is far more opaque
at 85 GHz compared to 19 and 37 GHz, and can cause
severe biases in geophysical surface parameters obtained
from 85 GHz SSM/I data, particularly in cloud-covered areas.
However, if the atmospheric conditions are obtained from other sources,
or have negligible variations in the region studied, this channel can
well be used for sea ice observations.
A procedure to retrieve the total sea ice concentration
from a spaceborne dual-polarized passive microwave instrument
operating near 90 GHz was first developed by
Svendsen et al. (1987).
A physical basis to interpret 85 GHz brightness temperature
in terms of
total and multiyear ice concentration was presented
by Lomax et al. (1995). They compared the Svendsen
et al. algorithm (SVA) and the NTA estimates
of total ice concentrations and found an
excellent agreement over cloud-free areas of high
ice concentration in winter. The agreement remained good for
cloudy scenes in winter but larger discrepancies occurred
in summer.
Lubin et al. (1997) compared
ice concentrations retrieved from 85 GHz SSM/I data
using the SVA with shipborne
ice observations during Arctic summer
revealing an agreement that was at least as
good as that obtained with NTA ice concentrations.
Markus and Burns (1995) and Hunewinkel et al.
(1998) developed methods to detect polynyas and to
derive high resolved sea ice edges from the
37 and 85 GHz channels of the SSM/I, respectively.
These methods can not be used to calculate the sea
ice concentration, but
to classify open water, the interior ice pack,
and new ice.
Kern (2000) developed
a weather-correcting algorithm to calculate the total
sea ice concentration
(SEA LION algorithm)
using the normalized polarization difference at
85 GHz together with monthly tie points, which are
reference brightness temperatures the for two ocean surface
types of the Antarctic: open water and ice.
The SEA LION algorithm includes a weather correction scheme
based on radiative transfer modelling and
atmospheric data calculated from the other SSM/I channels
or taken from numerical weather prediction models.
Kern and Heygster (2001) compared the SEA LION, NTA, and Bootstrap algorithm
(BTA) (Comiso et al. 1997) ice concentrations in the Antarctic
with ship observations revealing the most convincing linear
regression with the SEA LION algorithm.
The SEA LION ice concentration of the Antartic
averaged over 1992-1999 is about 3% smaller (5% larger) than
corresponding BTA (NTA) ice concentrations.
However, the quality of the SEA LION ice maps strongly depends
on the reliability of the involved atmospheric data.
Moreover, the correction of the 85 GHz SSM/I data for the
weather influence requires to handle data from several different sources
making the sea ice concentration retrieval time consuming.
4. ASI Algorithm
The ARTIST Sea Ice (ASI) algorithm is a hybrid algorithm
combining the SVA used for ice-covered
regions with the NTA algorithm used for the ice-free ocean.
This approach takes advantage of the low
sensitivity of the 19 GHz channels to atmospheric effects
and of the high resolution of the 85 GHz channels.
A basic assumption of the SVA is that the atmospheric
influence can be represented by a smooth function
(third-order polynomial) between the ice and the ice-free ocean.
The microwave radiative transfer equation is expressed in
a simplified form as defined in Svendsen et al. (1987)
P=c(a C+b) (3)
where C is the ice concentration,
P is the difference between the vertically and
horizontally polarized 85 GHz brightness temperatures,
and a,b, and c are parameters depending on
sea ice and water emissivities, ice temperature and
the atmospheric optical depth.
Equation (3) was derived assuming
a plane parallel atmosphere
over a Lambertian surface with the effective
temperature being constant with height
and with a viewing zenith angle near 50°.
In order to derive the four coefficients
d0,d1,d2 and d3
of the above mentioned third-order polynomial
C(P)=d3 P3 + d2 P2 + d1 P +
d0 (4)
one has to estimate the tie points
P0 and P1 for the totally ice-free and ice-covered
ocean, respectively. The partial derivatives of the
ice concentration dC/dP constrain an equation system
dC(P)/dP=b/(a P0) for C=0% (5)
dC(P)/dP=(1+b/a)/P1 for C=100% (6)
for totally ice-free (eq. 5) and ice-covered (eq. 6) ocean.
The fit of a third-order polynomial function C(P) through
C(P0)=0 and C(P1)=1 with
dedicated slopes (eqs. 5 and 6)
yield the desired coefficients d0,d1,d2 and d3.
The implementation of this method is straightforward
with the ratio b/a=-1.14 given
by Svendsen et al. (1987) for typical sea ice signatures.
The selection of proper tie points P0 and P1
is crucial, because they include the
complete radiative physics empirically.
In order to account for the
variability of the atmosphere, Svendsen et al. (1987)
proposed a self-adapting method to calculate
tie points for each orbit separately
by "setting P1 equal to the median of
a certain number of the smallest P,
and P0 equal to the median of the largest P".
However, Lubin et al. (1997) found that
physically meaningful total ice retrievals were obtained
without varying the tie points even
during arctic summer with frequently overcast conditions.
We propose a new, simple method for the estimation of reasonable
tie points for the 85 GHz algorithm, which avoids the a
priori selections of regions well inside and well
outside the ice but requires reference ice concentration
data C(x) obtained using a well-proven method.
These could stem either from lower resolved satellite
data or from higher resolved (airborne) data.
The data have to be on the same grid with matched resolution
(degraded for the higher resolved data).
Our proposed method includes the following steps:
1.) Choose initial tie points P0 and P1.
2.) Calculate the sea ice concentration C(ASI).
3.) Calculate the least-squares fit parameters SLOPE and OFFSET
from C(x) and C(ASI).
4.) Vary the tie points P0 and P1.
5.) If not (SLOPE~1 and OFFSET~0) goto 2.).
Hereby C(ASI) is the ice concentration defined by eqs. (4)
and (7). The estimation of tie points by calculating
the median of some samples implies the samples to be suitable
and well distributed, which may be in general not the case.
The usage of a least-squares statistics
with independent reference data
rather than the selection of just two points should
provide more robust and accurate results for the tie points,
as the results shown in the next section will confirm.
Svendsen et al. (1987) and Lubin et al. (1997)
suggested to use the 85 GHz algorithm in conjunction with lower
frequency observations to reduce large errors
caused by weather effects.
We follow these suggestions by using
the NTA over ice-free areas.
Applying the following rule to each pixel of
ice concentration maps derived with the SVA and the NTA:
C(ASI):=0, for C(NTA) <= T
C(ASI):=C(SVA), for C(NTA) >= T (7)
C(NTA) and C(SVA) are the ice concentrations calculated
with the NTA and the SVA, respectively, and
T=30% is a threshold to masks
ice-free areas as seen with the lower frequency channels.
For this approach, C(SVA) and C(NTA) have to be mapped
into the same grid.
For the present study we use a polar stereographic projection
according to Snyder (1982) and a gridding and interpolation method,
which is part of the free software package Generic Mapping Tools GMT
(Wessel and Smith, 1998; GMT).
In order to generate a smooth and
differentiable interpolation the gridding was performed
with continuous curvature splines in tension
(Smith and Wessel, 1990).
We used a grid cell size of 200 m for comparisons
between ice concentrations derived from aircraft and
from SSM/I measurements as well as between SSM/I and ERS-2 SAR data.
A grid cell size of about 8 km was used to ingest the
SSM/I ice concentrations into the numerical atmospheric
models.
The sea ice edge obtained from the 19 GHz channel
data can be expected to be located farther away
from the pack ice if compared to 85 GHz channel data.
For instance C(SVA) may be already 0% while C(NTA)
still is 30% (see Fig. 6).
In general the full range (0-100%) of ice concentrations
is detectable despite of the rigid threshold cut-off T=30% (eq. 7).
However, isolated ice patches in the ice-free ocean may be lost.
The local variability of the atmosphere
and the radiation properties of water and ice are not considered
using the SVA.
A detailed analysis of the resulting errors
was done by Svendsen et al. (1987)
and by Lubin et al. (1997).
5. Validation
The ice concentrations derived from aircraft measurements
have been taken as a reference
in order to obtain the tie points P0 and P1 of the ASI algorithm
with the previously described least-squares method.
When comparing aircraft and satellite data the different
spatial resolutions of the sensors have to be taken into account.
In order to adjust the aircraft data to the effective field of view
of the SSM/I,
they have been smoothed with a Gaussian weighted filter.
In the following the results of April 1st (microwave radiometer)
and 4th (optical line scanner) are discussed in more detail.
5.1. Validation with aircraft passive microwave measurements
A cloud free situation south-east of Svalbard
on April 1st was used to fly three long legs over the
ice edge zone in Storfjorden.
The flight track of the Polar 4 aircraft is shown in Figure 1.
The measurements started at 10:45 and ended at 14:45 UTC
yielding profiles of surface microwave radiances.
The measurements were interrupted by calibrations.
Therefore the total duration of the time-series (Fig. 2 and 4)
is reduced to about three hours
corresponding to a total distance of 689 km.
Ice concentrations were derived from the AWI radiometer data
with the NTA algorithm, henceforth denoted aircraft data
C(Aircraft radiometer; NTA).
In order to check their consistency C(Aircraft radiometer; NTA)
values have been compared to ice concentrations
derived with the NTA from SSM/I data C(SSM/I; NTA).
The mean difference between
C(Aircraft radiometer; NTA) and C(SSM/I; NTA)
is less than one percent (-0.5%) with a standard deviation
of ~5% (Fig. 2).
A quite high correlation coefficient CC between
both data sets of 0.98
legitimates the applied resolution matching technique.
A least-squares fit of both data sets
reveals
C(Aircraft radiometer; NTA)=1.0818 C(SSM/I; NTA)-0.06
The same set of tie points
(see Cavalieri et al., 1991) has been
used for aircraft and satellite data.
The atmospheric influence valid for the flight level of
the SSM/I is included into the NTA tie points.
The AWI radiometer has been operated at a lower altitude
with a lower atmospheric influence due to
the shorter path length through the atmosphere.
While SSM/I data include the influence over the entire
atmospheric depth the aircraft data are only influenced
by the atmosphere below the aircraft.
This effect can be expected to be substantially smaller.
However, the mean difference in the obtained
ice concentrations is very small, especially
for high concentrations, and therefore, the above-mentioned
difference has been neglected in
further calculations.
In a next step the aircraft data C(Aircraft radiometer; NTA)
have been used together with the SSM/I 85 GHz data in order
to derive tie points for the ASI algorithm as previously described.
The tie points which provide the best linear fit
of about 55 data points (averaged aircraft ice concentration
profiles and co-located SSM/I ice concentration pixels)
are:
P0=47 K (open water)
and
P1=7.5 K (ice).
From these tie points we obtain the coefficients
for the third-order polynomial
d0=6.45714*10-06, d1=-0.000605256, d2=-0.00922521, d3=1.10031
and calculated ice concentrations (eqs. 4 and 7)
henceforth denoted as C(SSM/I; ASI), C(ASI) or ASI data.
The mean difference between C(Aircraft radiometer; NTA) and
C(SSM/I; ASI) is less than one percent (-0.6%)
with a standard deviation of ~6% (Fig. 4).
The correlation coefficient CC=0.97 between both data sets
reveals a linear relationship of the results from the
different sea ice algorithms NTA and ASI (Fig. 5).
These tie points have been used for all day of this study
except for April 4th and 5th where line scanner
data was used.
Furthermore, we constructed automatic processing
routines for the production of sea ice maps
as a first try of using these tie points throughout all
seasons for both hemispheres (http://www.seaice.de).
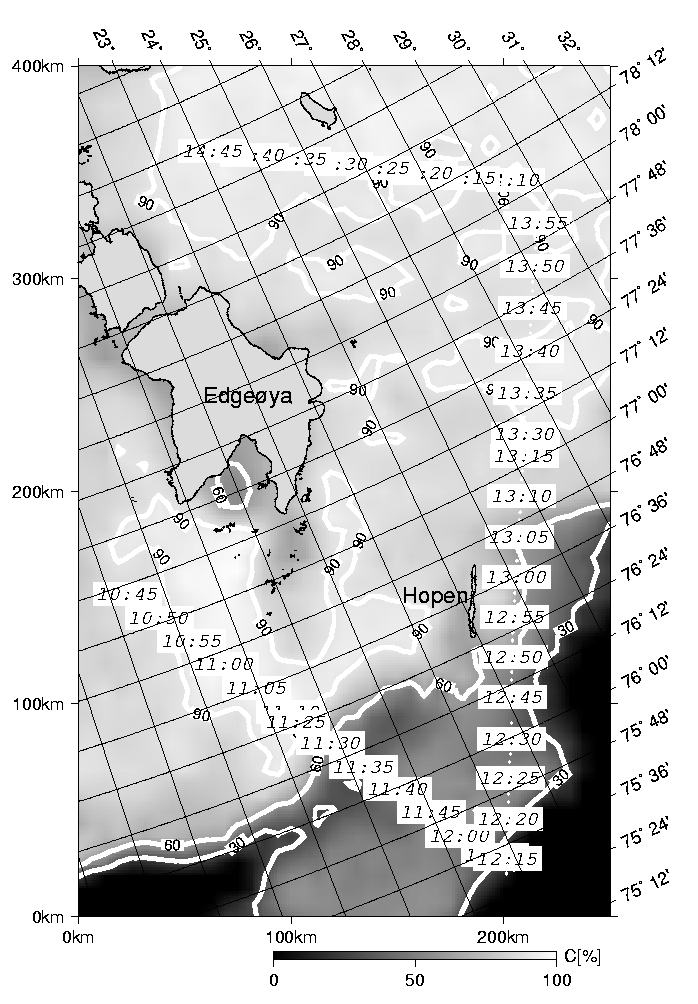
Figure 1: Flight track of AWI Polar 4 research aircraft operating
the dual-polarized 19 and 37 GHz AWI radiometers
superimposed on the ice concentration map calculated with the ASI algorithm.
Isolines are given in addition.
The shown area is mainly covered with first-year ice.
Only the area south of Hopen island consists of pancake ice.
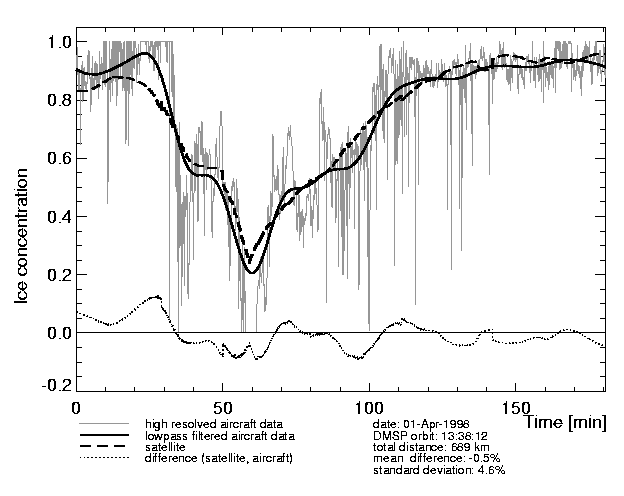
Figure 2: Ice concentrations C(Aircraft radiometer; NTA) and C(SSM/I; NTA)
derived from aircraft and satellite measurements using the NTA.
The difference between the SSM/I and the lowpass-filtered aircraft data
is also indicated.
The time-series were constructed from seven measurement intervals
of the profile shown in Figure 1 (10:43-11:12, 11:24-11:45, 11:59-12:08, 12:12-12:33,
12:44-13:16, 13:26-13:57, 14:09-14:47).
For this reason slight disconuities appear in the curve obtained
from the satellite profile.
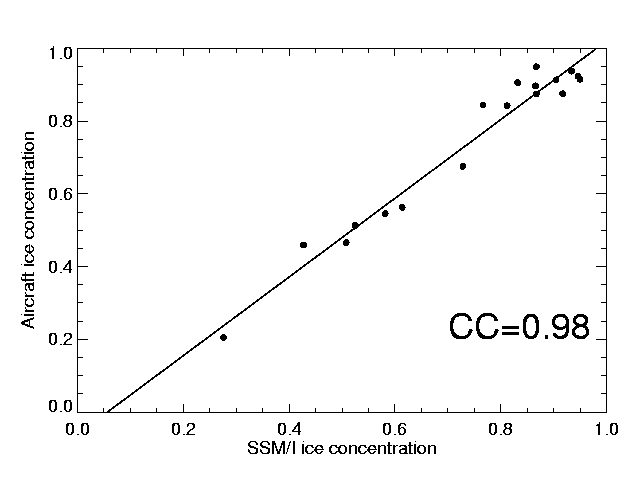 Figure 3: Aircraft data averages C(Aircraft radiometer; NTA)
and the co-located SSM/I ice concentration C(SSM/I; NTA).
Figure 3: Aircraft data averages C(Aircraft radiometer; NTA)
and the co-located SSM/I ice concentration C(SSM/I; NTA).
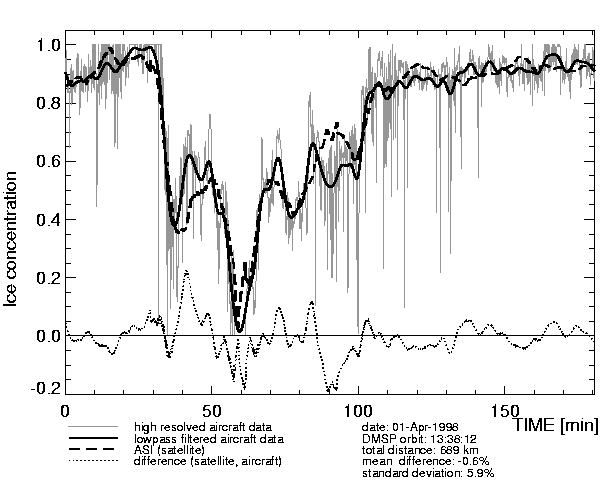
Figure 4: Ice concentrations C(Aircraft radiometer; NTA) and C(SSM/I; ASI).
The high resolved aircraft data are identical to those of Figure 2b.
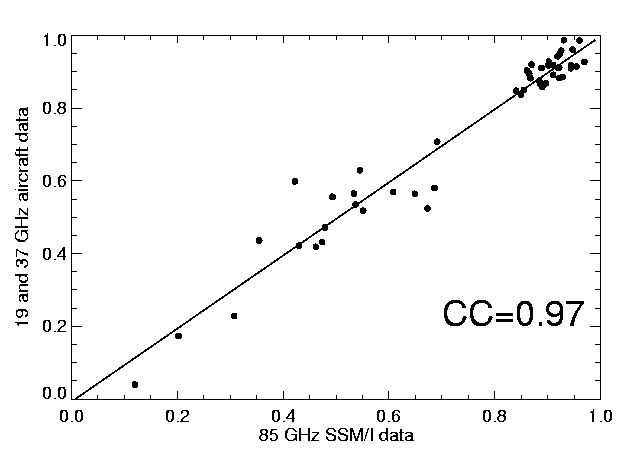 Figure 5: Aircraft data averages C(Aircraft radiometer; NTA)
and the co-located SSM/I ice concentration C(SSM/I; ASI).
The linear regression line is almost the identity because the
ASI tie points have been selected that way in order to
obtain the perfect fit.
Figure 5: Aircraft data averages C(Aircraft radiometer; NTA)
and the co-located SSM/I ice concentration C(SSM/I; ASI).
The linear regression line is almost the identity because the
ASI tie points have been selected that way in order to
obtain the perfect fit.
5.2. Validation with aircraft optical line scanner measurements
On April 4th two research aircraft (Polar 2 and 4)
flew a coordinated mission along the fifth meridian in
a convective atmospheric boundary layer (ABL) during a cold air outbreak.
Sea ice information across the MIZ was obtained over a distance of 38 km
on Polar 2 using the optical line scanner system.
The ice concentration derived from line scanner data C(Aircraft line scanner)
were used in order to estimate the tie points for the ASI
algorithm similarly as demonstrated in the
previous section (Bochert, 1999):
P0=50.23 K (open water)
and
P1=12.3 K (ice).
From these tie points we derived the corresponding coefficients
d0=1.82546*10-05, d1=-0.00196167, d2=0.0362013, d3=0.817535
and calculated ice concentrations C(SSM/I; ASI) (eqs. 4 and 7).
These values were used for the atmospheric
modelling studies on April 4th and 5th 1998.
The mean difference between C(Aircraft line scanner) and C(SSM/I; ASI)
is less than one percent (-0.4%) with a standard deviation of four percent.
The resulting ASI ice concentrations are in general 10-20%
higher than those obtained with NTA for pack ice regions.
The tendency of these results agrees with comparisons
of NTA and optical satellite images reported
by Steffen and Schweiger (1991) and Comiso et al. (1997).
6. Comparisons to ERS-2 SAR images
There are no established algorithms available for
to estimate the ice concentration from
ERS-SAR images due to the limitation of: only one vertically
polarized C-band channel, the steep incidence angle,
ambiguities in sea ice surface and volume scattering effects,
wind speed depending ocean clutter and the presence of
speckle noise (Bochert, 1999).
Nevertheless, ERS-SAR images carry
valuable spatially high-resolved information, which
can be accessed by visual inspection.
In this study, ERS-2 SAR images have been used
in a more qualitative manner for a
consistency check.
We present two cases observed with ERS-2 SAR and SSM/I,
the MIZ in the Fram Strait and the Storfjorden Polynya.
6.1. Evolution of the MIZ in the Fram Strait
The higher spatial resolution achieved if using the SSM/I 85 GHz data
to retrieve maps of C(SSM/I; NTA) and C(SSM/I; ASI)
is demonstrated by comparing the results with two different ERS-2 SAR
images obtained in the Fram Strait north-west of Svalbard.
A compact ice edge zone resulting from on ice flow
during the previous days is evident in the ERS-2
SAR image of March 30th 1998 (Fig. 6, top).
Then a low pressure system east of Svalbard
and high pressure over Greenland lead to
northerly winds shifting the ice edge southwards
and transforming the formerly compact
ice edge zone into a diffuse one (Fig. 6, bottom).
The average distance between the 30% to the 60% isolines was taken
as a measure for the width of the MIZ and is shown in Table 2.
The sharp gradient of the ASI ice concentration on March 30th
decreases during the week and changed by a factor of 3.5
on April 6th.
In comparison, the NTA ice concentration gradient
has changed lesser (factor 1.6)
because of the lower spatial resolution of the 19 GHz channels.
The difference in the spatial resolution is exemplified
by the number of independent measurements for the 5000 km²
area which is shown in the top image of Figure 6; this area is
covered about twice (32 fold) by the effective field of view
of the 19 GHz (85 GHz) channels.
Table 2: Changes in MIZ width as observed from space
with different spatial resolutions
| Algorithm |
Resolution |
Date |
State |
Width |
Change |
| ASI | 12 km | March 30th | Compact | 6.6 km | - |
| ASI | 12 km | April 6th | Diffuse | 23.3 km | 3.5x |
| NTA | 50 km | March 30th | Compact | 24.5 km | - |
| NTA | 50 km | April 6th | Diffuse | 38 km | 1.6x |
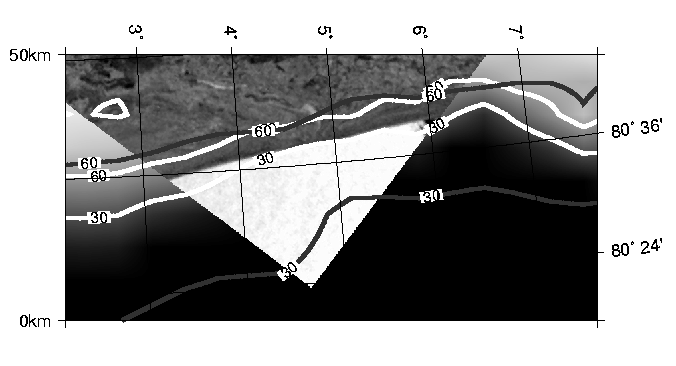
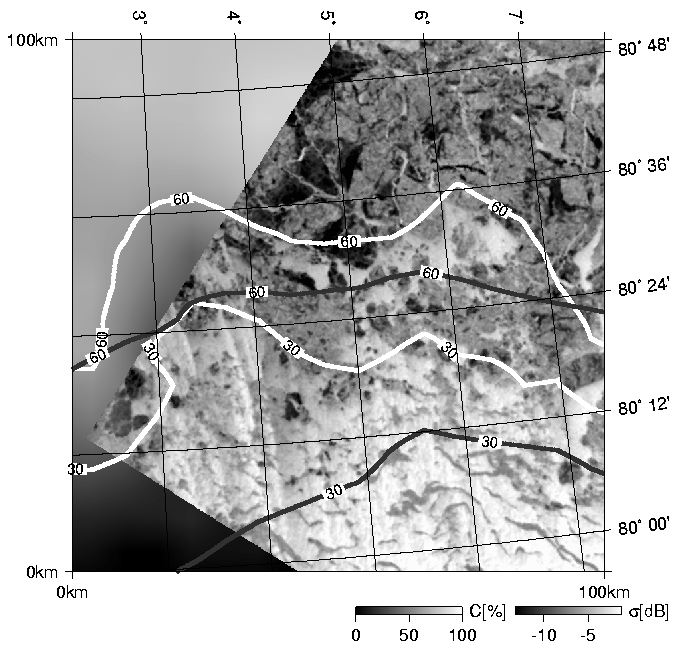
Figure 6. The marginal ice zone:
SAR images recorded by ERS-2 on March 30th, 1998
(top, orbit:15380, frame:1935)
and on April 6th, 1998 (bottom, orbit:15480, frame:1953)
The ERS-2 SAR images are
overlain by ice concentration isolines
from the ASI algorithm (light) and NTA (dark).
In areas not covered by the SAR images,
the ice concentration C(SSM/I; ASI) is displayed in a gray scale.
(Original ERS-SAR images (C)ESA 1998).
6.2. Storfjorden Polynya
A persistent latent heat polynya in Storfjorden, Svalbard, was observed by
ERS-2 SAR imagery during the winter 1997/1998 (Haarpaintner, 1999).
Since the temporal coverage of Storfjorden by ERS-2 SAR data is of
the order of two weeks, the ERS-2 SAR observations were combined with
models and in situ data to quantitatively
describe the importance of the polynya for the
total ice production and bottom water formation from induced brine release
in this area (Haarpaintner et al., in press).
In order to replace or support the rather infrequent SAR observations
with an approach, which allows more frequent observations,
we made some initial attempts of using SSM/I data for this purpose.
Figure 7 presents the ice conditions in Storfjorden
on April 9th, 1998, observed with ERS-2 SAR.
We manually segmented the ERS-2 SAR image of Figure 7
in order to derive a thematic map consisting of three classes:
fast ice, pack ice and polynya (Haarpaintner, 1999).
The polynya class was defined in a fuzzy sense,
and contains brash ice, new ice, nilas or young ice
in addition to open water areas.
A more concise classification of the polynya ice types
is not feasible using ERS-2 SAR images due to
ambiguities of the radar backscatter.
The thematic map is shown in Figure 8 together with ice
concentration isolines derived from SSM/I data.
The northern part of the fjord (north of 78 °N) and the
eastern coast of Spitsbergen were covered by fast ice of about 120 cm
thickness. A flaw polynya developed from the fast ice southwards to about
77° 30' N. Similar conditions were observed from a helicopter flight
during fieldwork on April 15th.
According to the observations and the models, the
Storfjorden polynya was composed by about equal areas
of open water and thin ice,
which is in good agreement with the average ASI ice
concentrations.
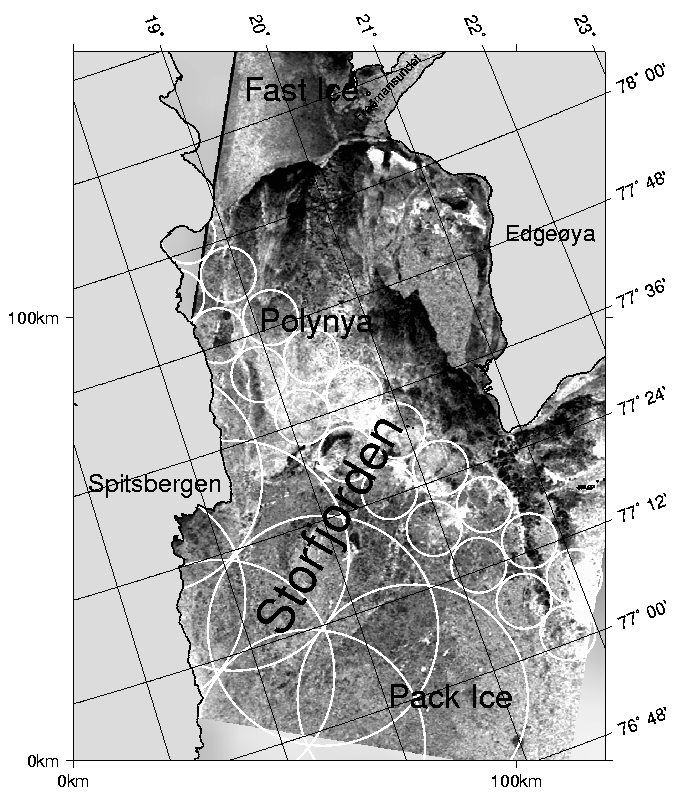 Figure 7: ERS-2 SAR image, April 9th, 1998.
It shows the Storfjorden polynya, extending
southward from the fast ice region in the north.
The circles exemplify
the different effective fields of view and sample distances
of the SSM/I at 19 GHz (50 km circles) and 85 GHz
(12 km circles). (Original ERS-SAR images (C)ESA 1998).
Figure 7: ERS-2 SAR image, April 9th, 1998.
It shows the Storfjorden polynya, extending
southward from the fast ice region in the north.
The circles exemplify
the different effective fields of view and sample distances
of the SSM/I at 19 GHz (50 km circles) and 85 GHz
(12 km circles). (Original ERS-SAR images (C)ESA 1998).
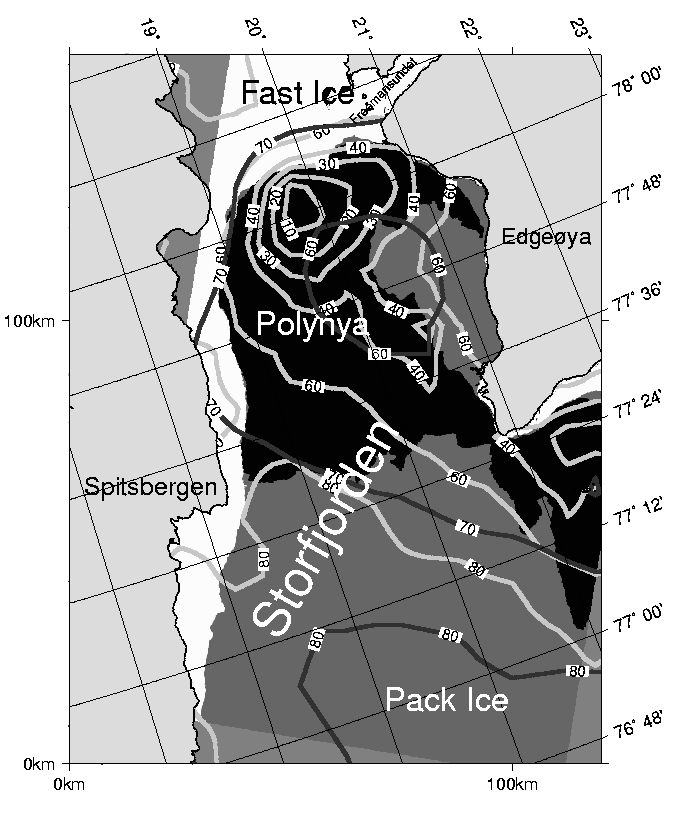 Figure 8: Segmented ERS-2 SAR image (white: fast ice, dark grey:
pack ice, black: polynya), April 9th 1998.
It is superimposed with the sea ice concentration C(SSM/I; NTA) (dark grey)
and C(SSM/I; ASI) (light grey).
Figure 8: Segmented ERS-2 SAR image (white: fast ice, dark grey:
pack ice, black: polynya), April 9th 1998.
It is superimposed with the sea ice concentration C(SSM/I; NTA) (dark grey)
and C(SSM/I; ASI) (light grey).
7. Modelling of the atmospheric boundary layer over the marginal sea ice zone near Svalbard
The heat exchange between atmosphere and ocean is strongly influenced by
the sea ice concentration.
Regional atmospheric models use grid sizes
of about 20 km and thus ice concentration data are needed in a
similar resolution. In the following two subsections the results of
two different mesoscale atmospheric models are discussed.
The principal improvements that can be expected from
high resolution ice data, such as obtained from the ASI algorithm, are
further demonstrated.
7.1. Flow parallel to the ice edge over Storfjorden
The air flow over the ice-edge zone in Storfjorden was simulated using a
two-dimensional hydrostatic mesoscale ABL model (Savijärvi, 1991).
The present model version
has 92 points with a 2 km grid length in the horizontal, and 50 levels in the
vertical, and the flow is forced by a geostrophic wind at a height of 3 km.
The sea ice concentration is prescribed and applied when calculating
the grid-averaged surface fluxes by the mosaic method (Vihma, 1995).
On March 30th, 1998, an aircraft flight mission was made over the
Storfjorden (Hartmann et al., 1999): it was observed that the
ABL flow was parallel to the ice edge,
and the leads were 10 to 20 K warmer than the near-surface air. Two otherwise
identical model simulations were made: in the first one the ice concentration
was based on the ASI algorithm, and in the second one on the NTA. The ice
concentrations differed substantially from each other, the NTA producing a more diffuse
ice edge zone (Fig. 9 a). The results of the observed and modelled air
temperature at a height of 40 m are shown in Figure 9 b. We see that the air
temperature is closely related to the ice concentration in both simulations.
The observed air temperature has a strong gradient in the ice edge zone.
This is well reproduced in the simulation based on the ASI data but not in
the one based on the NTA. In the zone where the ice concentrations differ from
each other (from -60 to 70 km in Fig. 9), the mean absolute deviation between
the observed and modelled air temperature is 0.7 K for the ASI-based results and
1.7 K for the NTA-based results. In the 50 km wide zone of the largest
difference, the corresponding numbers are 0.8 K and 3.1 K, respectively.
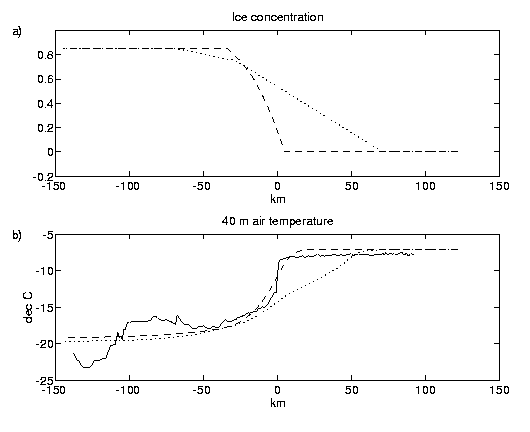
Figure 9: (a) Ice concentrations used in the model simulations based on the ASI
algorithm (dashed) and NTA (dotted), (b) observed (solid)
and modelled (ASI: dashed, NTA dotted) 40 m air temperatures over the ice
edge zone in Storfjorden on March 30th, 1998.
7.2. Off-ice flow over the Fram Strait
The non-hydrostatic mesoscale model METRAS
(Schlünzen, 1990; Lüpkes and Schlünzen, 1996) was applied in a
2D version to simulate the flow across the MIZ
northwest of Svalbard at about 80° N 7° E using a
horizontal resolution of 8 km and 14 grid layers below 500 m height.
Figure 10 shows a comparison of
aircraft observed ice concentration C(Aircraft line scanner)
data with satellite estimates C(SSM/I; NTA) and C(SSM/I; ASI).
Obviously the NTA algorithm underestimates the concentration for
values higher than 0.5 whereas ASI data
(interpolated on the model grid) are close to the observations.
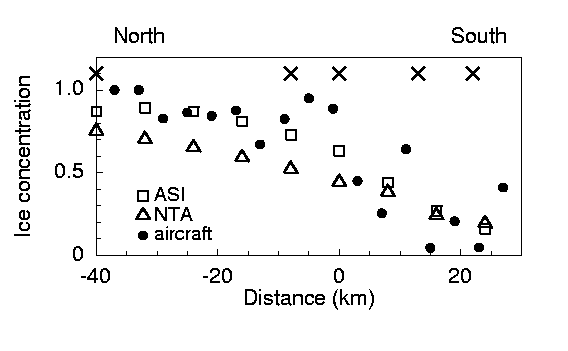
Figure 10: Ice concentration on April 5th 1998 obtained with the two different
algorithms. Crosses denote locations of aircraft observed temperature profiles (see Fig. 11).
At the considered day (April 5th 1998) a cold-air outbreak had
developed with off-ice northerly winds across the MIZ.
These conditions always lead to strong convection over the
MIZ due to the strong difference between the near-surface air
temperature and that of the water surface.
The aircraft measured also profiles of potential
temperature at the positions marked by crosses in Figure 10.
Figure 11 shows the observed profiles and model results
which have been obtained with the two different sea ice algorithms.
The first profile refers to the northernmost position at -40 km in Figure 10,
the profile on the right hand side is at the southern end of the MIZ (position 22 km).
It is quite obvious that observations and model results are in better
agreement when the ASI ice concentration C(SSM/I; ASI) are applied.
A similar result was obtained for the April 4th 1998
(not shown here).
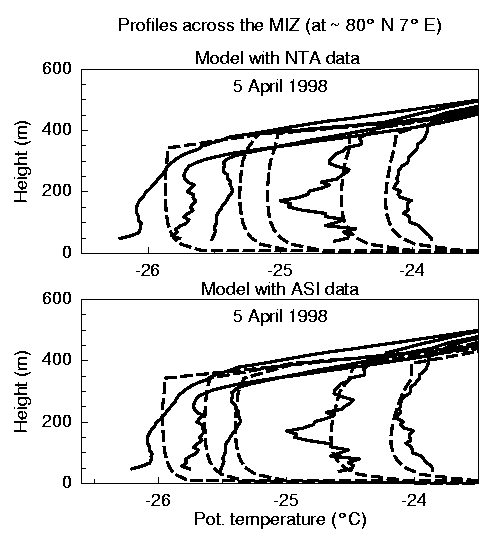
Figure 11:
Observed (solid) and modeled (dashed)
profiles of the potential temperature obtained from METRAS with ice concentration
boundary conditions from different ice algorithms.
Positions of profiles are marked with
crosses in Figure 10, first profile on
the left is at the northern end.
8. Discussion and Conclusions
Aircraft flights in March and April 1998 during the
Arctic Radiation and Interaction Study
provided high resolution sea ice data.
We used the NASA Team (NTA) algorithm to derive ice
concentrations from aircraft based dual
polarized 19 and 37 GHz radiometer data and to
to verify and validate a hybrid SSM/I algorithm.
The ARTIST Sea Ice (ASI) algorithm
combines the high resolution
(12 km) of the 85 GHz channels with the lower weather dependency
of the NASA Team (NTA) algorithm for reliable open water/ice discrimination.
We derived tie points for the ASI algorithm
with the aid of a linear regression method and aircraft data.
By that way unreliable a priori guesses of regions well inside
and well outside the ice for the tie point selection have been avoided.
Very high correlations
CC=0.97 and CC=0.98 have
been obtained from a 689 km
aircraft profile and co-located SSM/I ice concentration pixels
calculated with ASI and NTA, respectively.
The mean differences between aircraft and satellite data were
for both algorithms less than one percent with standard deviations
of about five percent.
We derived an alternative set of tie points for the ASI algorithm
by using aircraft optical line scanner images.
Ice concentrations calculated with the ASI algorithm and
these tie points were not afflicted with low concentration biases
typically associated with the presence of thin ice types
as that obtained from NTA.
We used ERS-2 SAR images to support qualitatively
the interpretation of ASI and NTA sea ice maps.
We found that the 85 GHz channels are suitable
to resolve mesoscale ice features. We demonstrated
how the state of the ice edge (diffuse or compact) can
be observed in ASI ice maps. Moreover, we found that
the SSM/I is suitable for observations of coastal zone polynyas.
We investigated the heat budget of the ABL in two case studies.
In both, the model runs applying the ice concentration
data based on the ASI
algorithm agreed better with the observations than those based on
the NTA data.
It is interesting to note that the ABL was sensitive to the ice
concentration data of two very different cases.
On March 30th 1998, in the Storfjorden, the wind was parallel to the ice edge,
while on April 5th an off-ice flow took place over the Fram Strait.
Furthermore, the results were obtained
using two different models: a hydrostatic one with a first-order
turbulence closure and a non-hydrostatic one with an
advanced turbulence closure. Thus, the
importance of the spatial resolution of the sea ice concentration data
in ABL models is neither restricted to certain flow conditions nor to a certain kind of
atmospheric
models.
We conclude that the ASI algorithm is practical for field studies
where extensive high resolution ice concentration
data are required and some independent ice concentration
measurements are available for the estimation of
well adapted tie points.
The calculation of ice concentrations is quite simple and
straightforward, thus the operational usage of the ASI algorithm is feasible
(see http://www.seaice.de).
However, the validity of ASI results depends on the weather conditions.
For instance, passing fronts may cause large
errors in the obtained ice concentrations.
And there is an obvious need for further validation
studies, especially for other regions, seasons, and
weather conditions.
Acknowledgments
The authors are grateful to all the people who contributed
to the successful completion of the ARTIST campaign.
In particular, we thank the crew of the Polar 2 and 4
research aircraft. We also thank Pete Conway of
Earth Systems Science Lab at the
University of Alabama, Huntsville, for providing SSM/I
ground pass times which were used for flight planning;
Søren Andersen of the Danish Meteorological Institute
for the recording of the SSM/I single swath data;
Stefan Kern of the Institute of Environmental Physics,
University of Bremen, Germany, for numerous comments and discussions;
Klaus Künzi for hosting Lars Kaleschke in the
Institute of Environmental Physics,
University of Bremen, Germany.
The ARTIST project was funded by the Commission of the European Community
under contract Nr.
ENV4-CT97-0497-0487 (DG12-ESCY).
The Storfjorden work was funded by grant contract Nr.
MAS3-CT96-5036 from the Commission of the European Community
and grant of Norwegian research council 127802/720
under contract
with the Norwegian Polar Institute, Tromsø.
ERS2-SAR images of
Storfjorden were distributed by the Tromsø
Satellite Station
and weather data from Hopen by the Norwegian
Meteorological Institute (DNMI).
References
Aagaard, K., and Carmack, E.C. (1989).
The role of sea ice and other fresh water in the arctic circulation,
Journal of Geophysical Research, Vol 94, No. C10, pp. 14485-14498.
Bochert, A. (1999).
Airborne line scanner measurements for ERS-1 SAR interpretation
of sea ice,
International Journal of Remote Sensing, Vol. 20, No. 2, pp. 329-348
Birnbaum, G. , Lüpkes, C. (submitted).
A new parameterization of surface drag in the marginal sea ice zone,
submitted to Tellus.
Burns, B.A. (1993).
Comparison of SSM/I ice-concentration algorithms for the Weddell Sea,
Annals of Glaciology, Vol. 17, pp. 344-350.
Cavalieri, D.J., Gloersen, P., and Campbell W.J. (1984).
Determination of sea ice parameters with the NIMBUS 7 SMMR,
Journal of Geophysical Research, Vol. 89, No. D4, pp. 5355-5369.
Cavalieri, D.J., Crawford, J.P., Drinkwater, M.R., Eppler, D.T., Farmer, L.D.,
Jentz, R.R., and Wackerman, C.C. (1991).
Aircraft Active and Passive Microwave Validation of Sea Ice Concentration
From the Defense Meteorological Satellite Program Special Sensor Microwave
Imager,
Journal of Geophysical Research, Vol. 96, No. C12, pp. 21989-22008.
Cavalieri, D. J. and S. Martin. (1994)
The contribution of Alaskan, Siberian and Canadian coastal polynyas
to the halocline layer of the Arctic Ocean,
Journal of Geophysical Research, Vol. 99, No. C9, pp. 18343-18362.
Comiso, J.C., Cavalieri, D.J., Parkinson, C.L., and Gloersen, P. (1997).
Passive Microwave Algorithms for Sea Ice Concentration: A Comparison
of Two Techniques,
Remote Sens. Environ., Vol. 60, pp. 357-384.
Haarpaintner, J. (1999).
The Storfjorden polynya: ERS-2 SAR observations and overview,
Polar Research, Vol. 18, No. 2, pp. 175-182.
Haarpaintner, J., Gascard, J.-C., and P. M. Haugan.
Ice production and brine formation in Storfjorden,
Journal of Geophysical Research, in press.
Hartmann, J., Albers, F., Argentini, S., Bochert, A., Bonafe, U., Cohrs, W.,
Conidi, A., Freese, D., Georgiadis, T., Ippoliti, A., Kaleschke, L., Lüpkes,
C., Maixner, U., Mastrantonio, G., Ravegnani, F., Reuter, A., Trivellone, G.,
and Viola, A. (1999).
Arctic Radiation and Turbulence Interaction Study (ARTIST),
Reports on Polar Research, No. 305,
Alfred-Wegener-Institute for Polar and Marine Res.,
Bremerhaven, Germany.
Hunewinkel, T., Markus, T., Heygster, G.C. (1998).
Improved Determination of the Sea Ice Edge with SSM/I Data
for Small-Scale Analysis.
IEEE Transactions on Geoscience and Remote Sensing, Vol. 36, No. 5., pp. 1795-1808
Hollinger, J.P., Peirce, J.L., and Poe, G.A. (1990).
SSM/I instrument evaluation.
IEEE Transactions on Geoscience and Remote Sensing, Vol. 5, No. 28, pp. 781-790.
Kern, S. (2000).
Sea ice concentration derived using SSM/I 85.5 GHz imagery.
Proc. of a Workshop on Mapping and Archiving of Sea Ice
Data - The Expanding Role of Radar,
JCOMM Technical Report No. 7, WMO/TD-No. 1027, pp. 179-184.
Kern, S., and Heygster, G. (2001).
Sea ice concentration retrieval in the Antarctic
based on the SSM/I 85.5 GHz polarization.
Annals of Glaciology, in press.
Proc. of a Workshop on Mapping and Archiving of Sea Ice
Data - The Expanding Role of Radar,
JCOMM Technical Report No. 7, WMO/TD-No. 1027, pp. 179-184.
Kramer, H.J. (1996).
Earth Observation Remote Sensing, 3rd edition,
Berlin, Heidelberg, Germany: Springer-Verlag.
Ledley, T.S. (1988).
A coupled energy balance climate - sea ice model: impact of
sea ice and leads on climate,
Journal of Geophysical Research, Vol. 93, No. D12, pp. 15919-15932.
Lubin, D., Garrity, C., Ramseier, R. and Whritner, R.H.. (1997).
Total Sea Ice Concentration Retrieval from the SSM/I 85.5 GHz
Channels during Arctic Summer,
Remote Sens. Eviron., Vol. 62, pp. 62-76.
Lüpkes, C., Schlünzen, K.H. (1996).
Modelling the Arctic convective boundary layer with
different turbulence parameterizations.
Boundary-Layer Meteorol., Vol. 79, pp. 107-130.
Schlünzen, K.H. (1990).
Numerical studies on the inland penetration of see
breaze fronts at a coastline with tidally flooded mudflats.
Beitr. Physik Atm., Vol. 63, pp. 244-256.
Markus, T., Burns, B.A. (1995).
A method to estimate subpixel scale coastal polynyas with
satellite microwave data.
Journal of Geophysical Research, Vol. 100, No. C3, pp. 16707-16718.
Markus, T., and Cavalieri, D.J. (2000).
An Enhancement of the NASA Team Sea Ice Algorithm,
IEEE Transactions on Geoscience and Remote Sensing,
Vol. 38., No. 3., pp. 1387-1398.
Martin, S., and Kauffman, P. (1981).
A field and laboratory study of wave damping by grease ice,
J. Glaciol., Vol. 27, No. 96, pp. 283-313.
Savijärvi, H. (1991).
The United States Great Plains diurnal ABL variation and
the nocturnal low-level jet,
Mon. Wea. Rev., Vol. 119, No. 3, pp. 833-840.
Snyder, J.P. (1982).
Map Projections Used by the U.S. Geographical Survey,
Geological Survey bulletin 1532, Second edition, United States
Government Printing Office, Washington
Wessel, P., and Smith, W.H.F. (1998).
New, improved version of Generic Mapping Tools released,
EOS Trans. Amer. Geophys. U., Vol. 79, No. 47, pp. 579.
Smith, W. H. F, and Wessel, P. (1990).
Gridding with continuous curvature splines in tension,
Geophysics, No. 55, pp. 293-305.
Steffen, K., and Schweiger, A. (1991).
NASA team algorithm for sea ice concentration retrieval from defense meteorological satellite program Special Sensor Microwave Imager: Comparison with Landsat imagery,
Journal of Geophysical Research, Vol. 96, No. C12, pp 21971-21987.
Svendsen, E., Mätzler C., and Grenfell, T.C. (1987).
A model for retrieving total sea ice concentration from a spaceborne dual-polarized passive microwave instrument operating near 90 GHz,
International Journal of Remote Sensing, Vol. 8, No. 10, pp. 1479-1487.
Vihma, T. (1995).
Subgrid parameterization of surface heat and momentum fluxes over polar oceans,
Journal of Geophysical Research, Vol. 100, No. C11, pp. 22625-22646.












